Uncertainty Quantification (UQ) is the process of measuring the uncertainty in the parameters of a physical model that are calibrated on experimental observations. Statistical (e.g. Bayesian) inference is one of the standard techniques for UQ that incorporates both expert knowledge (prior) and experimental measurements (likelihood). The uncertainty in the parameters can be propagated to any quantity of interest, achieving updated robust predictions. In addition, UQ offers the model evidence, a measure of fitness of the model to the data.

Our plan is to develop efficiently parallelized optimization and sampling algorithms casted in terms of Bayesian UQ. Other ML methodologies, related also to the field of molecular modelling by trying to augment the classical physics-based potentials, will be implemented using supervised and/or unsupervised learning, such as the Neural Networks, Gaussian process regression, SVM, etc.

The data-driven variational inference will be described and implemented via a “Digital Twin” paradigm, shown below. In more detail, we propose work in the following areas:

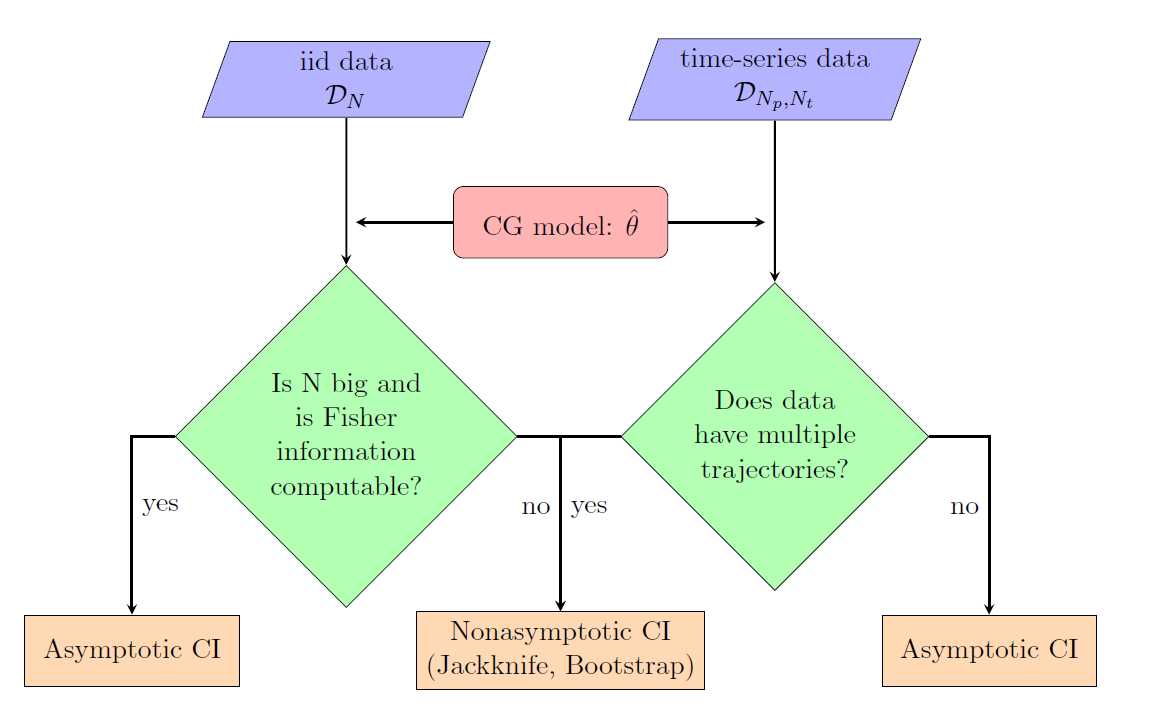
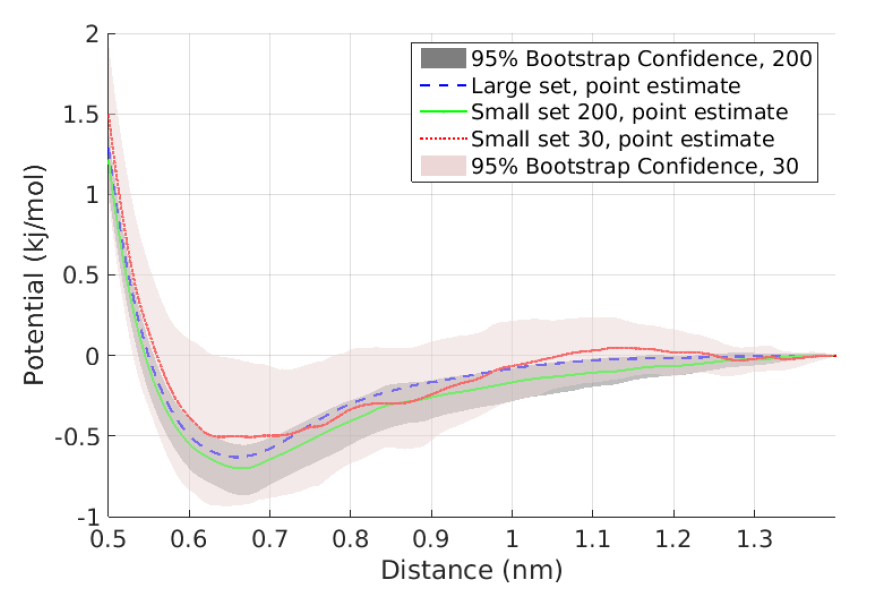
• Data-driven confidence interval estimation in coarse-graining: Due to the limited availability of fine-grained data, the quantification of induced errors in bottom-up systematic CG models is still an unexplored area of mathematical CG. Here, we propose new methodologies and algorithms for the quantification of confidence in bottom-up coarse-grained models for molecular and macromolecular systems, based on rigorous statistical methods. The proposed method is based on a statistical framework recently developed in our research centre in which statistical approaches, such as bootstrap and jackknife, are applied to infer confidence sets for a limited number of samples, i.e. molecular configurations. Moreover, we gave asymptotic confidence intervals for the CG effective interaction, assuming adequate sampling of the phase space.

These approaches have been demonstrated, for both independent and time-series data, in a simple two-scale fast/slow diffusion process projected on the slow process. They have also applied on an atomistic polyethylene (PE) melt as the prototype system for developing coarse-graining tools for macromolecular systems. For this system, we estimate the coarse-grained force field and present confidence levels with respect to the number of available microscopic data. The above approaches will be extended to deal with more challenging multi-component nanostructured heterogeneous materials, as those described in Themes 1 and 3, and also for systems under non-equilibrium conditions (eg. shear flow).

• Force field Selection and Sensitivity Analysis of model parameters via information-theory approaches: Furthermore, we will derive a systematic parametric sensitivity analysis (SA) methodology for the CG effective interaction potentials derived n the framework of the current project. Our SA method is based on the computation of the information-theoretic (and thermodynamic) quantity of relative entropy rate (RER) and the associated Fisher information matrix (FIM) between path distributions, that has been applied before by us on two different molecular stochastic systems, a standard Lennard-Jones fluid and an all-atom methane liquid. The obtained parameter sensitivities were compared against sensitivities on three popular and well-studied observable functions, namely, the radial distribution function, the mean squared displacement, and the pressure. Here, we will extend this approach for multi-component nanostructure systems.

In addition, the above methods will be combined with the Hierarchical Bayesian framework to be used as a selection tool for (a) force field selection in MD simulations using heterogeneous data and (b) for the selection of the appropriate coarse-grained model for a given system.