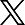Project description

The motion of a liquid droplet over a solid surface is a process that is commonly observed, for instance, with water dew on plant leaves or rain drops on a car's windshield. These scenarios are incredibly easy to visualise, yet, they are inherently complicated to study due to the competition of effects that operate across multiple scales and in the vicinity of the solid/liquid/vapour contact line. The understanding of such phenomena is crucial for the development of many technologies, such as within self-cleaning surfaces, DNA analysis, printing applications, hydrogen fuel cells, desalination and water harvesting systems for arid regions across the planet. Many of these technologies are developed based on intuition derived from an amalgamation of laboratory experiments, mathematical modelling, and computer simulations. Although impressive progress has been made in both software/algorithms and hardware, computer simulations may require days to complete on supercomputers, even when investigating relatively simple cases. The combination of mathematical and data-driven modelling approaches can constitute an effective tool for the development of low-order, surrogate models, as a means to mitigate the computing requirements, and, importantly, to enhance our understanding of the key physics that drive droplet motion. In this project, the synergies between applied mathematical analysis, data-driven modelling approaches and large scale simulations will be explored for wetting phenomena. The development of novel modelling and computational tools in the form of open-source software will allow us to enhance our fundamental understanding of how to control droplet transport in complex environments, to investigate several industrially relevant scenarios, aspiring to contribute towards a more cost-effective development of new technologies and the optimisation of existing ones.

Objectives

Through synergistic physics-based and data-informed modelling approaches, the key objectives of the project are

• Develop surrogate models for isolated droplets to be used as replacements for expensive direct numerical simulations;
• Assess and possibly extend regimes of applicability of surrogate long-wave models, which are often used for simulations of thin droplets;
• Pursue parametric studies for uncovering optimal mechanisms for droplet transport.

The prototypical scenarios under investigation include studies with sessile, partially wetting droplets on heterogeneous surfaces with (labels in the list below map to each of the sub-figures in Figure 1):

(a) Body forces. We will consider the inclusion of gravitational effects and body forces arising due to low-frequency vibrations on inclined and horizontal surfaces;

(b) Electric fields. The case of a leaky dielectric droplet in an ambient leaky dielectric fluid under a time-varying electric field applied in the direction normal to two parallel electrodes will be considered. Neglecting magnetic fields, the charge relaxation time scales are much longer than the magnetic time scales), the electric potential Φ must be determined as part of the solution, accounting for the corresponding Maxwell stresses at the interface.

(c) Evaporation/condensation in a pure vapour atmosphere. Droplets are in a pure vapour atmosphere on a substrate maintained at a fixed temperature, Ts, causing evaporation or condensation depending on its magnitude relative saturation temperature. By neglecting convective heat transport effects, the energy equation governing the temperature field, T, in the domain obeys Laplace’s equation, coupled with the appropriate BCs accounting for mass transfer

(d) Diffusion-limited evaporation. An alternative evaporation mechanism to be treated is the diffusive transport of from a drop towards the far-field. The vapour concentration, c, needs to be determined as part of the solution, assuming that its value in the far-field is constant, but below the saturation concentration. Such a non-equilibrium state induces a diffusive transport of liquid from the drop with mass flux j = −D∇c, where D is the diffusion coefficient.

The team for CODETHREE consists of researchers with expertise in applied mathematical analysis, large scale computing and fluid dynamics from The Cyprus Institute, Imperial College London and the Aristotle University of Thessaloniki.

Code development

High-performance computing codes are being developed using the open source software Basilisk for the simulation of droplets in various scenarios. Results of sample simulations with long-wave models are shown below. The codes will be made publicly available shortly after the project concludes.

Figure 2: (a) Adaptive mesh for droplets on an inclined surface, which is automatically coarsened away from the contact line. (b) Simulation snapshot of condensing droplets on an inclined surface, which is decorated with stripes of alternating wettability. For clarity, the precursor film is not shown.

The Team

• Nikos Savva
• Yiannis Vrionis
• Andreas Demou
• Alexis Provatas
• Collaborators
  • Demetrios Papageorgiou
  • George Karapetsas
• Former members: Antonis Pantelouris

Recent News

• July 2024: New article accepted to appear to the International Journal of Thermofluids (Job well done Yiannis!)
• April 2024: New article accepted to appear at the Mathematics journal (Congrats Andrea!)
• March 2024:  Alexis Provatas has been selected to participate in the 14^th International High Performance Computing (HPC) Summer School 2024, in Kobe, Japan, hosted by the RIKEN Center for Computational Science! The summer school will familiarize the best students in computational sciences with major state-of-the-art aspects of HPC and Big Data Analytics for a variety of scientific disciplines, catalyze the formation of networks, provide advanced mentoring, facilitate international exchange and open up further career options.
• October 2023: Success story featured on the EuroHPC website!

Conferences & Workshops

• “Dynamics of a partially wetting droplet on a chemically heterogeneous surface evaporating in a pure vapor atmosphere”, 14th Euromech Fluid Mechanics (Athens, GR, September 2022).
• “Dynamics of partially wetting droplets in the presence of complexity”, NANOMEC workshop, “Computational Modelling of Heterogeneous Materials: from Atomistic to the Engineering Scale”, The Cyprus Institute (March 2023).
• P. Y. Vrionis "Long Wave dynamics in heterogeneous environments” Basilisk (Gerris) Users’ Meeting, Paris, France (July 2023).
• Minisymposium organisation for the Micro & Nano Flows conference, Padova Italy: Contact Line Dynamics in Heterogeneous Environments (September 2023)
  • N. Savva “Asymptotic Methods for Reduced-order Modelling of Partially Wetting Droplets”
  • P. Y. Vrionis "Towards a flexible, highly-scalable, general-purpose thin film solver”
• N. Savva, “Asymptotic modelling for the spreading of a thin viscous drop on a chemically heterogeneous surface by gravity and surface tension”, 76th Annual Meeting of the Division of Fluid Dynamics, Washington DC, USA (November 2023).
• Strong Team Presence at the International Workshop on “Computational Modeling of Molecular Systems: From Atoms to the In-silico Design of Materials” (May 2024)
  • Posters
    • A. Pantelouris: "Application of Temporal Bundling and Pushforward Trick, within the Fourier Neural Operator (FNO)"
    • A. Provatas: “Simulating Evaporating Droplet Dynamics on Chemically Heterogeneous Substrates”
  • Talks
  • N. Savva: "Modelling And Simulation of Droplets in Heterogeneous Surfaces”
  • P. Y. Vrionis “Studying Condensation Dynamics on Inclined, Chemically Heterogeneous Substrates”
  • A. Demou: “Modeling Droplet Movement using Data-Driven and Existing Reduced-Order Models”
•  Forthcoming!
  • 1st European Fluid Mechanics Conference, Aachen, Germany (September 2024 - N. Savva)
  • ParCFD conference (September 2024 - A. Demou, P. Y. Vrionis)

Outreach

• The Cyprus Institute sCYence Fair (April 2023; April 2024).
• Innovation Workshop and Speed Networking Event
• Researcher's Night (September 2023)

Open Access Publications

• Demou & Savva (2024) Hybrid AI-Analytical Modeling of Droplet Dynamics on Inclined Heterogeneous Surfaces, Mathematics 12(8), 1188. (Data repository)