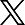The main scientific goal in this topic is to develop and use multi-scale computational (HPC + data-driven) methodologies in order to construct more accurate quantitative models of complex materials across different scales. To achieve this, a hybrid physics-based data-driven paradigm is proposed that links High-Performance Computing (large-scale simulations) with AI technologies. In more detail, we envision work along the following directions:
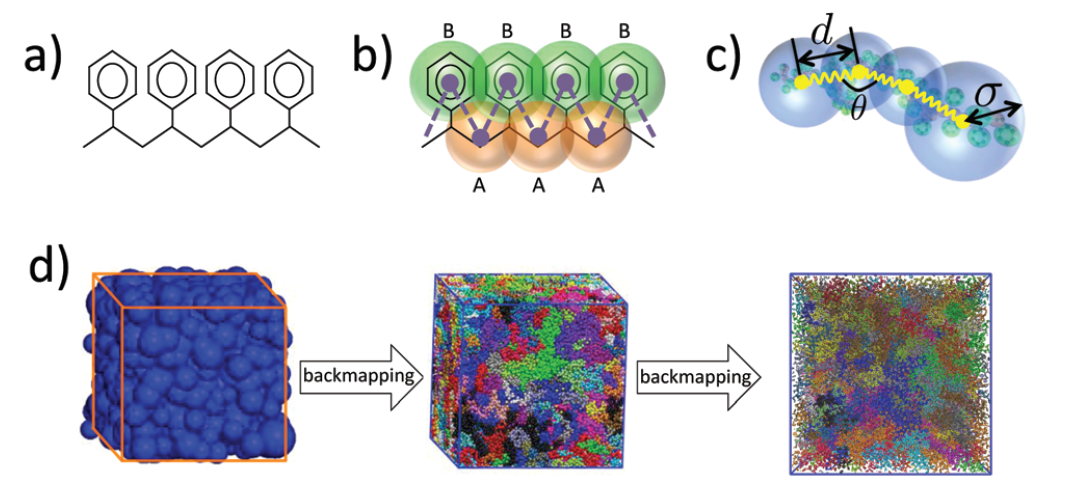
- Data-driven coarse-graining strategies: The development of data-driven systematic CG techniques is a very important and still unexplored area of multi-scale modelling. In systematic “bottom-up” strategies, the effective CG interactions are derived as follows: Assume a microscopic system, composed of N atoms/particles in the canonical ensemble, described by a Hamiltonian HN in the microscopic q (3N) configuration (positions of all atoms), and a mesoscopic CG description of this system with M “superatoms” (M<N), and Hamiltonian HM, in the mesoscopic Q (3M) phase space.
The observable can be distribution functions (e.g. bonded distributions, pair correlation functions, g(r)), the total force acting on a CG particle, or the relative entropy, or Kullback-Leibler divergence, between the microscopic and the coarse space Gibbs measure. Despite the success of such methods, they become problematic for multi-component nanostructured systems (e.g. blends, interfaces, crystals, etc.) due to the complex heterogeneous structure of such systems at the atomic level. One of the reasons the above techniques fail is that the set of basis functions used to approximate the exact, but not computable, many-body PMF is not large enough.
To overcome the above limitations, our approach combines the existing schemes with deep learning-based approaches to provide more accurate and transferable approximations of the CG model (free energy surface, FES) under a broad range of conditions. For this, we propose the use of neural networks (NNs) that can, in principle, be used to fit any continuous function on compact subsets of Rn (see universal approximation theorem). However, the application thereof to describe the interaction between atoms or molecules is not straightforward, since NNs do not obey the required symmetries (such as permutation, translation, etc.) dictated by physical laws of nature. To this end, the NNs will be combined with proper transformations of the original data. We anticipate that new CG force fields will be a more accurate approximation of the “exact” many-body PMF, thus deriving more powerful and transferable CG models. In addition, we will explore CG density-dependent potentials in which density-dependent terms are used to approximate the exact many-body PMF in an analogous manner to classical density functional theory. Recently we have developed such CG models for homopolymer bulk systems. Here we will extend such potentials to complex nanostructured systems, also comparing against the data-driven (NNs-based) approximations.
- Linking microscopic and mesoscopic scales: The main challenge in the multi-scale modelling of complex materials is the systematic linking of the models across the different scales. For these, algorithms that either eliminate (dimensionality reduction) or re-introduce degrees of freedom (back-mapping process) are required. Recently, we have developed hierarchical back-mapping strategies incorporating generic different scales of description from blob-based models and moderate coarse-grained up to all-atom models (see Figure 3). The central idea is to efficiently equilibrate CG polymers and then to re-insert atomistic degrees of freedom via geometric and Monte Carlo approaches. Furthermore, more recently we introduced a general image-based approach for structural back-mapping from coarse-grained to atomistic models using adversarial neural networks.
These methods have been extensively tested for polymer melts of high molecular weight. Here, we will extend these methods to provide large all-atom configurations for heterogeneous nanostructured systems. This is a particularly challenging area due to the inherent complexities of such systems, which has not been addressed in the literature so far. The new methods will be thoroughly examined and validated by comparing their structural and conformational properties of the back-mapped model configurations with reference data from smaller systems, which are obtained directly from long atomistic simulations.